|
Hermann Karcher (emeritus 2004)
Mathematisches Institut der
Universität Bonn
Endenicher Allee 60
53115 Bonn
Arbeitszimmer: Endenicher
Allee 60, Zimmer 3.007
Telefon: +49 228 73-2841, Geschäftszimmer: 73-2204
e-mail:
(.gif, please do not store in computer readable lists.)
I continue to use this e-mail address.
I no longer check spam, thus may loose some mail.
Meine Arbeitsgebiete waren:
Riemannsche Geometrie und Untermannigfaltigkeiten.
Warum ich von 1999 bis 2019 Schul- und Hochschulpolitik ignoriert habe:
Mitteilungen der Deutschen Mathematiker-Vereinigung 1998
2019 war das Kind im Brunnen und die Mitteilungen der DMV haben meine Klage darüber nicht veröffentlicht:
Sie werden es nicht glauben (2021):
Aus Schulbüchern - wirklich!
Von der Leiterin einer Praxis für Förderdiagnostik organisiert:
Auch andere sind entsetzt! (Stiehler 2021)
oder: Der langsame Tod der Analysis (Sonar 2012)
oder: Mathematische Fähigkeiten zu Studienbeginn (Schwenk 2013)
oder: Von allen guten Geistern verlassen (Wittmann 2014)
oder: Der Schwanz ist eine ... Exponentialfunktion (Lemmermeyer 2014)
oder: Entkernung des Mathematikunterrichts (Remus-Walcher 2016)
oder: Mathematische Schneeschmelze (Kaenders-Weiss 2017)
oder: Unser Schulsystem ist Mist (Lesch 2017)
oder: Fehlentwicklungen im Mathematikunterricht (Kühnel)
oder: Stochastik im Gymnasium - quo vadis? (Henze 2017)
oder: Bericht eines Studienberaters in Mathematik (Wagner 2019)
oder: Brief an Kultusministerkonferenz (Baumann, Schwenk, Spindler 2019)
oder: Aus der Spur - Zur heutigen Situation im Mathematikunterricht... (Wittmann 2021)
oder: Brief einer Studentin, erinnert an: Des Kaisers neue Kleider (persönlich 2022)
wide concern also in the US: Open letter with over 1780 signatures (June 2022)
or in France: Macron and the Villani Report (2017)
Ich habe angefangen,
Texte zur Schulmathematik zu schreiben. Inzwischen 15 Texte zu Analysis, Geometrie und Argumenten mit Zahlen,
als Gegenentwurf zu modernen Schulbüchern.
|
Hopf-fibered linked Tori aus
3D-XplorMath
Dies Apple Programm läuft auf neuen Maschinen nicht mehr (ab OS 10.15)
Image sequences made with this program are in virtualmathmuseum.org

The interactive Curves and Polyhedra of the museum are here (2021)
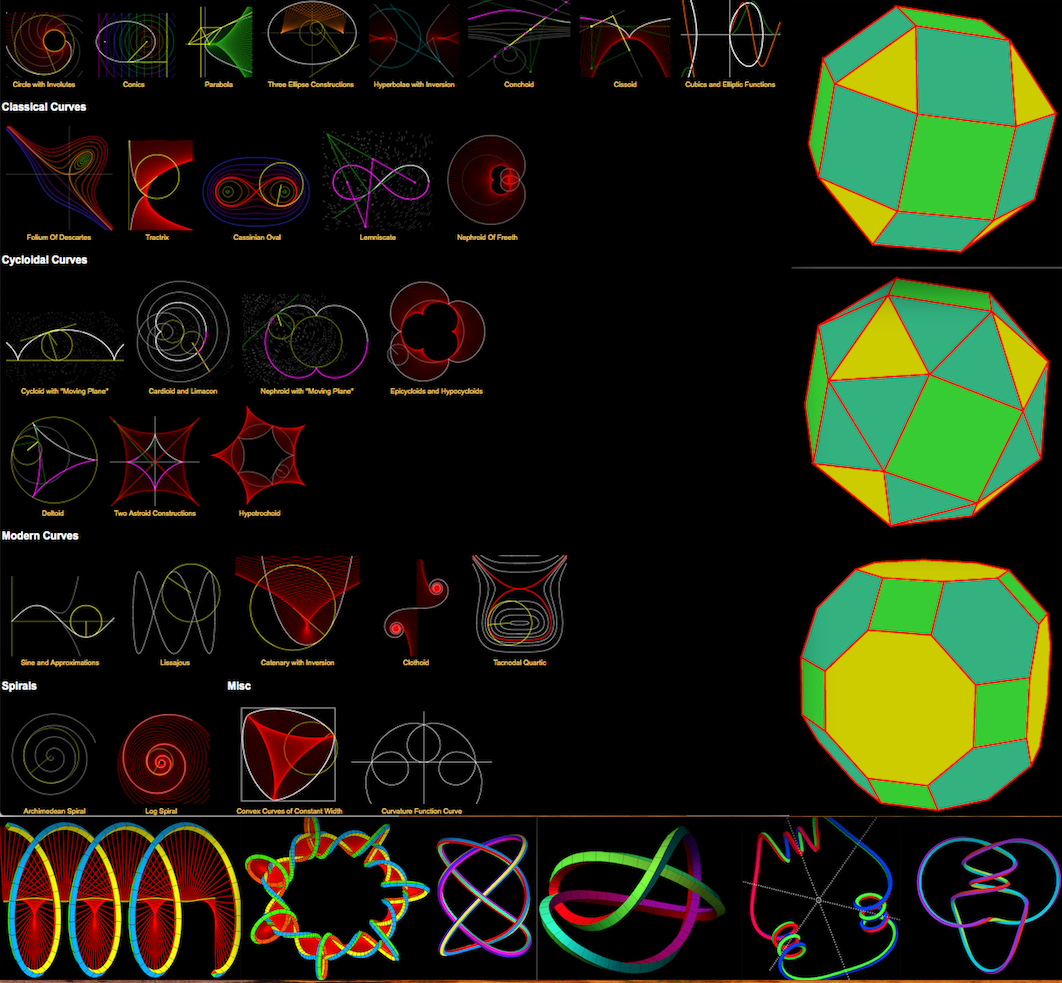
|
---------------------------
Correction (2014, ... 2022) ----------------------------
Wikipedia used to falsely write: Karcher means are a closely related
construction named after Hermann Karcher.
True and 2022 correctly quoted is: Karcher mean is the
renaming of the Riemannian Center of Mass construction
developed by Karsten
Grove and Hermann Karcher
in: How to conjugate C1-close group actions, Math.Z. 132, 1973, pp 11-20.
My 1977 paper with Riemannian Center of Mass
in the title is more easily found by google. But that does not
justify such a renaming. There I also quote: Grove, K., Karcher,
H., Ruh, E. A., Jacobi fields and Finsler metrics on compact
Lie Groups ..., Math. Ann. 211, 1974, pp. 7-21, where the
center is defined on SO(n) on much larger sets than can be done
with their Riemannian metric. In Buser, P., Karcher, H., Gromov's
Almost Flat Manifolds, Soc. Mat. France, Astérisque
81, 1981, the center is defined on nilpotent Lie groups just using
their connection, as in the Euclidean affine case. On spheres
the squared distance does not work so well since its Hessian has
different eigenvalues in radial and tangential direction. It is
easier, and even explicit, to use 1- cos(d(.,p)) instead, since
the minimum point of this function is the Euclidean center projected
from the midpoint back to the sphere. In Chern's book Global
Differential Geometry, MAA Studies in Mathematics, Vol 27,
1989, my article Riemannian Comparison Constructions explains
about such modified distance functions. The book is out
of print, but google finds my contribution
on my Homepage.
For more details see: Riemannian
Center of Mass and so called karcher mean (or: https://arxiv.org/abs/1407.2087)
-----------------------------------------------------------------------------------
-----------------------------------------------------------------------------------
Some Published and Unpublished Manuscripts,
small texts are still added (2020).
Information zu Vorlesungen WS 99/00 bis WS 03/04, Aufgaben,
Bilder, Texte.
Crystal Cove State Park: Photobook
(60 MB, 2011) of its fascinating Geology.
-----------------------------------------------------------------------------------
-----------------------------------------------------------------------------------
-----------------------------------------------------------------------------------
-----------------------------------------------------------------------------------
Ich prüfe seit 2007 nicht mehr.
Aus der Zeit vor der Bologna-Reform:
Ratschläge für Prüfungen
Zu meinen Matlabkursen.
Hochschulreform von außen und innen (analysis concepts).
Geometrisches Geschenk zu meinem 60. Geburtstag.
---------------------------------------------------------------------------------------
Am 13.5.02 war die Ehrenpromotion von
Frau Prof. Dr. Olga A. Ladyzhenskaya. Verbunden damit war die
Abschlußtagung (14.5.02) des SFB256.
Professor Dr. Olga A. Ladyzhenskaya,
7.3.1922 - 11.1.2004