The majority (63%) assess the quality of their Stage I studies as "rather bad" or "very bad".
The total average of the answers to question 1.1 is 2.31. Bonn and Köln are assessed not too bad.
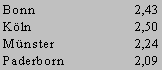
Prof. Dr. Paul Bungartz Tel.: 0228-73 22 11
Prof. Dr. Alexander Wynands -73 29 51
Faculty of Mathematical Studies Fax: 0228-73 79 16
University of Bonn wynands@math.uni-bonn.de
Beringstraße 6 bungartz@math.uni-bonn.de
53115 Bonn
Report on the responses to the question: April 1999
How do probationary teachers assess their study of Mathematics for Teaching at Sixth Form Level (Secondary School Level)?
In Summer 1998 interviews of probationary sixth form Mathematics teachers from 11 different teacher training colleges in NRW were held.
Summary.
Probationary teachers are very critical of their study of Mathematics for teaching at sixth form level.
Probationers
In total 176 probationary teachers answered the questions on the quality and content of their study.
174 people answered the question on their Age:
90 women between 25 and 40 years. Average age: 27.6 years; 8 were older than 30.
84 men between 25 and 40 years. Average age: 29.3 years; 20 were older than 30.
In addition to the probationary teachers, the Heads of Departments of Mathematics (Fachleiter) were interviewed.
In total, 12 of them answered the questions. The results of these interviews will be shown in italics in the following report.
The 176 probationary teachers were spread out over the 11 teacher training colleges as follows:
| City |
Bielefeld | Bonn |
Duisburg | Düsseld. |
Essen | Kleve |
Köln | Münster |
Paderborn | Siegburg |
Wuppert |
| Number of prob. teachers | 8 |
21 | 14 |
16 | 20 |
20 | 7 |
25 | 24 |
9 | 12 |
The following shows the number of probationary teachers who passed their First State examination at each University ...
Münster 41 Bonn 24 Köln 16 Paderborn 11
Düsseldorf 9 Bochum 8 Osnabrück 8 Wuppertal 8
Essen 6 Bielefeld 5 Dortmund5 Oldenburg 5
In addition, there were 18 Universities where less than 5 students graduated.
An overall view of the given questions and answers is shown below. The percentage for each given answer are shown.
Questionaire with percentage for each given answer:
Interviews of Mathematicians in teacher training colleges for sixth form level
We are interested in your opinion about the 1st part of the teacher training for sixth form level.
With your assistance this survey can help to optimise the study of teaching profession for sixth form level.
We thank you for your assistance.
Prof. Dr. P. Bungartz and Prof. Dr. A. Wynands Bonn, Summer term 1998
Your age: Average age: 28 years gender: m 84 f 90
Location of teacher training college : ___________ Start of your probationary period: month/year____ / ___
Where did you do your First State Examination ? Univ. of ______________________
When did you pass? ______________________
What else do you study apart from Mathematics: 2nd subject ________ if applicable 3rd subject _____
In which subject did you write your dissertation? about 20% in Mathematics.
Was the topic relevant to your teaching job?
not at all 36% rather not 35% rather yes 19% yes, very 10%
Which of your subjects do you like the most? Mathematics ca. 50% 2nd subject
1. Questions to your Stage I studies:
... overall as ...
very bad 10% rather bad 53% rather good 33% very good 4%
1.2 The Stage I studies were the same for all students of Mathematics. There was no distinction between the study for getting a diploma in Mathematics or studying for a teaching profession. From your perspective that is ...
very bad 28% rather bad 41% rather good 26% very good 5%
1.3 The demands of the subject Mathematics in the Stage I studies were ...
rather too low 1% rather too high 51% too high 21% appropriate 28%
1.4 The worksheets in addition to the lectures in Mathematics were overall ....
rather too easy 0% rather too difficult 58% too difficult 27% appropriate 15%
1.5 Do you think there should be written exams for every obligatory course during the Stage I studies?
not at all 7% on occasions 28% yes, definitly 42%
yes, if the intermediate examination would not be necessary any more 23%
2. Questions to your Stage II studies:
very bad 31% rather bad 48% rather good 18% very good 2%
2.2 To what extent was the teaching profession taken into account during your Stage II studies?
not at all 45% too little 51% sufficient 3% very much 1%
2.3 The demands of the subject Mathematics during your Stage II studies were ...
rather too low 0% rather too high 50% too high 32% appropriate 18%
2.4 Do you prefer lectures or seminars in Mathematics especially for trainee teachers
(seperated from Mathematics for a diploma) ?
not at all 2% rather not 4% rather yes 25% yes, definitly 70%
3. Questions on the Didactics of Mathematics and on Educational Studies
3.1 Did you attend courses on
general didactic problems of teaching Mathematics no 35% yes 65%
questions on the contents of sixth form teaching? no 39% yes 61%
questions on the contents of general secondary school level? no 46% yes 54%
3.2 How do you assess the quality of the courses on the Didactics of Mathematics which you attended concerning the job prospect of becoming a teacher? ... overall as ...
very bad 40% rather bad 44% rather good 16% very good 1%
not enough 60% rather not enough 30% often 9% very often 1%
3.4 Did you do a School placement in Mathematics ?
no 30% yes 70% if yes: How do you assess your placement?
overall it was ... not enough 52% rather not enough 30% rather enough 4% appropriate 15%
the quality was ... very bad 7% rather bad 30% rather good 48% very good 15%
3.5 What should the proportion be between the actual subject of Mathematics and the Didactics of Mathematics (which are related to teaching Mathematics but do not include general Educational Studies) during the first part of your teaching training in Mathematics for sixth form level?
100 : 0 0% 90 : 10 4% 80 : 20 10% 70 : 30 46% 60 : 40 41%
3.6 During your time at university you also had to study Educational Studies (ES) (in addition to Mathematics and your other subject) in the following proportion: 1st subject : 2nd subject : ES = 2 : 2 : 1.
The proportion of ES is ...
too high 11% rather too high 33% rather too low 41% too low 7% o.k. 8%
3.7 How do you assess your Educational Studies as job preparation for being a teacher?
... overall as ...
very bad 40% rather bad 48% rather good 10% very good 2%
4. Finally...
4. 1 The study of Mathematics should have given you mathematical competence. Was that achieved?
not at all 2% rather not 26% rather yes 57% yes, definitly 15%
The study of Mathematics should have given you self-confidence for your profession as a teacher. Was that achieved?
not at all 19% rather not 39% rather yes 39% yes, definitly 4%
4.2 Which subjects should be taught to new trainee teachers for sixth form level during their study of Mathematics.
(Please add courses if necessary!)
a) in Mathematics: Mathematical Logic 57% Analytical Geometry 77%
Differential Geometry 22% Theory of Probabilities 90%
Algebra 57% Topology 8% Number Theory 56% Numerical Maths 39% Function Theory 44% Measure Theory 7% (axiomat.) Geometry 39%
....................................................................... .............................
b) Didactics of..... Analysis 96% Li. Algebra 78% Numerical Maths 28%
Stochastics 87% Geometry 76% Arithmetic (for year 11-16) 38%
Algebra (for year 11-16) 61% Geometry (for year 11-16) 71%
Statistics/Probability (for year 11-16) 58%
.....................................................................................................
Topics on the Didactics of Mathematics:
Methodological problems in Teaching Mathematics 86% Theory of learning processes 38%
Questions to Psychological problems 48% Problems of Motivation 78%
Empirical Research in Teaching 21% School Placements 73%
........................................ ...............................................................
c) History of Mathematics 55%
Questions to Heads of Departments of Mathematics
Please let us allow to ask you the following questions:
When did you do your degree for the First State Examination? 19__ Where did you do your degree?________
What is your second subject besides Mathematics ? _____________ 3rd Fach? _______________
Was the topic of your dissertation
for the First State Examination relevant to your job as a teacher? yes___ no___
(comment:)_____________________________________________________________________________
should only be a subject related dissertation Yes__ No__
can either have an emphasis on a subject related topic or an emphasis on Didactics Yes__ No__
(Comment:)_______________________________________________________________________
2. The Stage I study in Mathematics should be the same for both, students in Mathematics (Diploma) and trainee teachers Yes__ No__
(Comment:)_______________________________________________________________________
3. The Stage II study should also be relevant to teaching profession
no, not at all__ on occasions __ often __ very often __
(Comment:)_______________________________________________________________________
4. How important do you think are teaching related practical experiences during the first period of teaching training at university?
very important __ important __ less important __ not important __
(Comment:)_______________________________________________________________________
5. How should be the proportion between the actual subject of Mathematics and the Didactics of Mathematics (which are related to teaching Mathematics but do not include general Educational Studies) during the first part of your teaching training in Mathematics for sixth form level?
100 : 0 90 : 10 80 : 20 70 : 30 60 : 40
(Comment:)_______________________________________________________________________
6. During the time at university trainee teachers also have to study Educational Studies (ES) (in addition to Mathematics and the other subject) in the following proportion: 1st subject : 2nd subject : ES = 2 : 2 : 1.
The proportion of ES is ... too high rather too high rather too low too low
(Comment:)_______________________________________________________________________
7. Which subjects should be taught to new trainee teachers for sixth form level during their study of Mathematics.
(Please add courses if necessary!)
a) in Mathematics: Mathematical Logic Analytical Geometry
Differential Geometry Theory of Probabilities
Algebra Topology Number Theory Numerical Maths
Function Theory Measure Theory (axiomat.) Geometry
....................................................................... .............................
b) Didactics of..... Analysis Li. Algebra Numerical Maths
Stochastics Geometry Arithmetic (for year 11-16)
Algebra (for year 11-16) Geometry (for year 11-16)
Statistics/Probability. (for year 11-16)
.....................................................................................................
Topics on the Didactics of Mathematics:
Methodological problems in Teaching Mathematics Theory of learning processes
Questions to Psychological problems Problems of Motivation
Empirical Research in Teaching School Placements
........................................ ...............................................................
c) History of Mathematics
The following shows the main
Results including short comments.
In total, the topic of the dissertation was for 70% of the trainee teachers "not at all" or "rather not" relevant for their later job as a teacher. The proportion of topics relevant to the teaching job varies from university to university: In Paderborn there were 5 out of 11 dissertations relevant to teaching, in Münster 12 out of 41, in Bonn 4 out of 24 and in Köln 2 out of 16.
Surprisingly (!?), only around 20% of the dissertations are written in Mathematics, although both chosen subjects are liked nearly equally among the students: favourite subject Mathematics: 45%, both subject equally liked: 5%.
Quality of the study
Question 1.1: How do you assess the quality of your Stage I studies as a basis for your training as a Mathematician and as a teacher?
In order to calculate the average on a scale from one to four the different answers (from left to right) are given appropriate numbers: 1 (very bad), 2 (rather bad), 3 (rather good) and 4 (very good ).
| The majority (63%) assess the quality of their Stage I studies as "rather bad" or "very bad". The total average of the answers to question 1.1 is 2.31. Bonn and Köln are assessed not too bad. |
|
Many of the students, who say that the demands of the Stage I studies are too high, assess maybe because of that !?- the quality of their Stage I studies as "rather bad" or "very bad". They do not understand enough and assess that as bad.
Question 2.1: Quality of the Stage II studies in Mathematics
| Even more (79%) assess the quality of their Stage II studies as "rather bad" or "very bad". The total average of the answers to question 2.1 is 1.92. Therefore Bonn with an average of 2.12 was assessed better than the three other universities with more than 10 probationers. |
|
For the assessment of Stage II studies it is even more obvious that:
Many of the students, who say that the demands of the Stage II studies are too high, assess the quality of their Stage II studies as "rather bad" or "very bad".
Question 3.2: How do you assess the quality of the courses on the Didactics of Mathematics which you attended concerning the job prospect of becoming a teacher?
| With 83% the quality of the courses on the Didactics of Mathematics is assessed as equally bad as the quality of the subject Mathematics. The total average is 1.77. Bonn with an average of 2.17 is assessed significantly better than the other three universities. |
|
The possibilities for attending courses on the Didactics of Mathematics obviously vary to a great extent from university to university, especially concerning School placements.
Whereas in Bonn only 2 out of 24 probationers did not attend courses on general didactic problems of teaching Mathematics (see question 3.1), 5 probationers did "not at all" attend courses to questions on the contents of sixth form teaching and only 1 probationer did "not at all" attend courses to questions on the contents of general secondary school level. In comparison, the values for the Universities of Münster and Köln are significantly lower. Especially worrying is the fact that only 50% of the students take part in School placements (see question 3.4).
Considering these results a lot of questions have to be asked such as:
How important do students and lecturers assess courses on the Didactics of Mathematics for trainee teachers in their first stage of their training?
To what extent do examination and study regulations differ from rated values and actual circumstances?
What are the examination topics for the teaching profession for the general secondary school level? Who are the examiners?
Question 3.4: Quality of School placements
| With about 64% the probationary teachers assess placements in Schools as "rather good" or "very good". The total average is 2.72. Bonn is in a leading position with an average of 2.91 for the quality and with also a high proportion of students who take part in School placements |
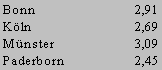
|
Frage 3.7: Quality of Educational Studies
| Considering the quality of the Educational Studies all universities were assessed as very bad. 88% assess the quality as "very bad" or "rather bad". The best university of the four is Paderborn. The total average is 1.74. |
|
Question 4.1: The study of Mathematics should give mathematical competence and self-confidence.
One major aim of the first training period is mathematical competence and self-confidence.
|
Despite criticism 71% of the probationers say their mathematical competence is now "rather good" or "very good". The total average is 2.84 and therefore higher than all other averages. |
|
It should be asked if there are not too many trainee teachers (28%) which did "not at all" or "rather not" achieve this aim.
The assessment of the mathematical competence is strongly correlated to the self-confidence for the job as a teacher.
| Only 42 % think that the study of Mathematics has given them a "rather good" or "very good" self-confidence. Or: More than 50 % think that they have not enough self-confidence. The total average is 2.27. |
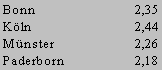
|
The correlation between self-confidence and mathematical competence is significant.
The attitude of having mathematical competence increases the self-confidence for being a teacher.
It is not possible to identify a correlation between self-confidence and the assessment of the demands of the Stage I studies. In addition there is no obvious correlation between the assessment of the Stage II studies and the active involvement in courses about teaching related problems. A weak correlation exists between the mathematical competence (as viewed by the trainee teachers themselves) and the assessment of the demands in the Stage II studies but not to the demands of the Stage I studies.
Taking into account the calculated averages for 7 "quality characteristics" shown above it is possible to identify the following
"University Ranking List" of the four universities which had more than 10 probationers.
| University |
#Proba-tioners |
Stage I studies |
Stage II studies |
Didactics |
School Plac. |
Sub-total |
Edu. Stud. |
Sub-total |
math. competence |
self- conf. |
total |
|
Bonn |
24 |
2.43 |
2.12 |
2.17 |
2.91 |
9.63 |
1.33 |
10.96 |
2.96 |
2.35 |
16.27 |
|
Münster |
41 |
2.24 |
1.93 |
1.32 |
3.09 |
8.58 |
1.68 |
10.26 |
2.83 |
2.26 |
15.35 |
|
Paderborn |
11 |
2.09 |
1.64 |
2.00 |
2.45 |
8.18 |
1.91 |
10.09 |
2.45 |
2.18 |
14.72 |
|
Köln |
16 |
2.50 |
1.38 |
1.25 |
2.69 |
7.82 |
1.27 |
9.09 |
3.13 |
2.44 |
14.66 |
|
Total |
ca. 170 |
2.31 |
1.92 |
1.77 |
2.72 |
8.72 |
1.74 |
10.46 |
2.84 |
2.27 |
15.57 |
Stage I studies Questions 1.2 to 1.5
The majority (about 70%) assess the combined Stage I studies with students studying Mathematics for a diploma (see question 1.2) as "rather bad" or "very bad".
Only 3 of 11 Heads
of Departments are against a combined Stage I study of Mathematicians studying
for a diploma and trainee teachers for sixth form level. Here are a few given
answers:
* this affirmation refers especially to trainee teachers for sixth
form level
* a reason for combined Stage I studies is the advantage of a possible change from studying for a trainee teacher to studying for a diploma
* yes, there is no harm.
70% think that the demands in Mathematics during the Stage I studies are "too high" or "rather too high" (see question 1.3). About 28% think that the demands are approriate.
Even more of the probationary teachers (about 85%) assess the worksheets to the lectures as "rather too difficult" or "too difficult" (see question 1.4). Only 15% think that they are appropriate.
Examinations (at the end of each semester) to obligatory lectures can help to assess mathematical ability and give orientation and experiences in written examinations. Only 6% think there should be no examinations at all. The proportion of students (42%), who think that there should be examinations is quite high.
Stage II studies Questions 2.2 to 2.4
90% think that the study of Mathematics does "not at all" or "not anough" integrate the prospect of becoming a teacher (see question 2.2).
7 of the 12 Heads of Departments think that content related to becoming a teacher should "often" be integrated and 4 emphasize that it should be "very often". Here are some of the comments:
* more applications of mathematical topics in Schools should be taught
* probationary teachers do not have a general overview about topics of teaching Mathematics.
82% think that the demands in Mathematics during the Stage II studies are "too high" or "rather too high; 18% think that the demands are "appropriate". That is 10% less than in the equivalent question of the Stage I studies. (see question 2.3 and 1.3).
Nearly all probationary teachers support the possibility of attending special lectures and seminars in Mathematics separated from students studying for a diploma (see question 2.4).
The Didactics of Mathematics and Educational Studies Question 3.1 to 3.7
The proportion of probationary teachers that did not attend courses on the Didactics of Mathematics is (too) high (see question 3.1).
39% were not taught anything about the contents of teaching topics for teaching at sixth form level; 46% considering the general secondary school level.
A lot of the probationary teachers would have liked to actively discuss (much more than it was possible) teaching related problems (see question 3.3). Only 10% had more chances to do so.
Placements in School (see question 3.4) are an obligatory part of study and examination regulations. However: Less than one third of the probationers had taken part in School placements during the first period of the teaching training. Is that an acceptable situation?
7 of the 12 Heads of Departments think that placements in Schools are "very important" for trainee teachers for sixth form level, 4 think that they are "important" and one thinks that they are "less important". Some of the comments:
* "the main advantage of School placement is the possibility of finding out if someone is actually suitable to the job"
* "unsuitable students can change their subject"
* "it should be possible to do such a placement in an early stage of the study so that someone can find out in time if he/she is suitable for the job."
More than 80% of the trainee teachers who took part in such a School placement think that the demands are too low and the period of time is too short.
The demand for a (much) greater proportion of courses on Didactics of Mathematics during the first period of the teacher training is very high. More than 90% would obviously like to attend much less courses in Mathematics, which cover about 85% to 90% (according to study regulations).
2 of the 11 Heads of Departments would like to have a proportion of 90 : 10 ( Mathematics : Didactics of Mathematics ), 2 would like to have a proportion of 80 : 20 and 7 would like to have at least 30% of courses on Didactics.
Some comments of the Heads of Departments:
* The topics of the courses on Didactics should be chosen so that they do not have to be examined.
* The quality of the courses on Didactics should be the main emphasis; An application to actually School related problems is often not possible.
* To know "what" is (at least) as important as to know "how".
* Many of the courses on Didactics, which I attended were not very helpful.
Many trainee teachers critisize the quality of the courses on Didactics. However, (or maybe because of that?) they would like to have much more and better options of courses on Didactics as a good preparation to the teaching profession at sixth form level.
The current proportion of Educational Studies of about 20% is assessed very differently (see question 3.6). 44% think that this proportion is "rather too high" or "too high". 41% think that it is "too low" or "rather too low".
7 of the Heads of Departments say that the proportion of Educational Studies is "too high" or "rather too high". 3 think that the proportion is "rather too low" and one person says it is "o.k."
Comments of the Heads of Departments:
* "The topics discussed in Educational Studies should be more relevant to problems in teaching.
* "...not efficient to the future job as a teacher."
* "The topics discussed in seminars are too theoretical and there are nearly no applications."
* "The proportion is obviously to low if, like it is possible in Köln, the examination in Didactics can be substituted by an examination in Mathematics and if the probationary teachers that I am currently teaching do not have a clue about general Didactics or even worse Didactics of Mathematics."
About half of the 88% of the people that made bad experiences in Educational Studies would like to have less courses in this area the other half would like to have significantly more. The meaning of such a study area for a teaching job in Mathematics for sixth form level seems to be very unclear. The need of action and change concerning study and examination regulations is obvious!