 |
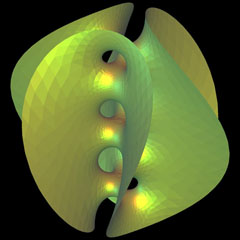
Less-Symmetric Scherk Saddle Tower
The classical minimal surfaces of H.F. Scherk were found around 1835
in an attempt to solve Gergonne's problem, a boundary value problem in the
cube. The Scherk surfaces were among the first candidates in Karcher's
experiments to modify the Weierstraß formula of existing surfaces. He
selectively increased or decreased symmetry, or twisted, or changed the
topological genus by inserting new handles. The less-symmetric saddle
tower originates from Scherk's saddle tower with triple symmetry and
modifying the asymptotic angle of the half plane wings. |
 |
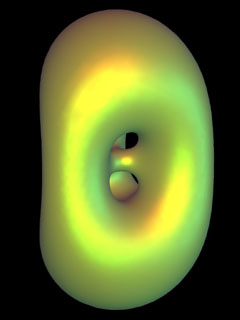
Chen-Gackstatter-Karcher-Thayer Surface Chen
and Gackstatter discovered in 1982 surfaces of genus one and two
each having an Enneper-type end of winding order three. Karcher found
that the end may be generalized to have any odd winding order. Thayer
constructed numerically surfaces with many more handles, i.e. higher
genus, up to 35, and each can have a generalized Enneper-type end.
The triply symmetric surface of the mobile has genus six and winding
order 5. |
 |
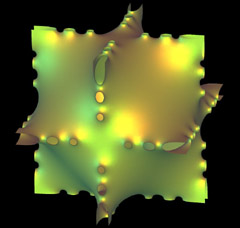
Lawson Surface of Genus 4
Lawson constructs compact minimal surfaces in the 3-sphere of arbitrary
genus by applying Morrey's solution of the Plateau problem in general
manifolds. This work of Lawson contains a rich set of ideas among
them the conjugate surface construction for minimal and constant mean
curvature surfaces. Karcher elaborated and perfected the conjugate
surface construction to allow the construction of a large number of
new minimal and constant mean curvature surfaces in different space
forms. |
 |
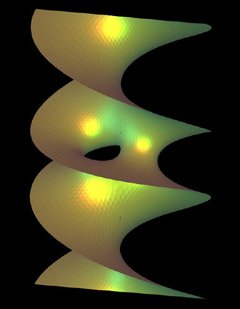
Neovius Surface with Additional
Handles In the last century H. A. Schwarz and his pupil
E. Neovius were among the first to specifically design new triply
periodic minimal surfaces using complex analysis and the Weierstraß
representation formula. The physicist A. Schoen found many more triply
periodic surfaces in crystallographic cells. Karcher elaborated the
conjugate surface construction to proof existence of Schoen's surfaces,
and many new examples. Karcher's modification of Neovius' surface
was numerically continued by Oberknapp to add a wealth of handles. |
 |
Hoffman-Karcher-Wei Helicoid
The Genus-One Helicoid
is a minimally embedded torus with one end and infinite total
curvature. More than 200 hundred years after the helicoid of Meusnier a
new embedded minimal surface with finite topology and infinite total
curvature was found in 1993. Crucial to their new discovery was the
characterization of the Gauss maps' essential singularity at the end
of the helicoid. It is known that the initiative to the genus-one
helicoid is due to Harold Rosenberg: "Hermann, why don't
David and you sit down and construct such an example?" |